[ADSP] 3과목 4장 통계분석 -2
회귀분석
회귀분석의 개요
회귀분석의 정의
- 하나나 그 이상의 독립변수들이 종속변수에 미치는 영향을 추정할 수 있는 통계기법
- 변수들 사이의 인과관계를 밝히고 관심있는 변수를 예측하거나 추론하기 위한 분석방법
- 독립변수의 개수가 하나이면 단순선형회귀분석, 독립변수의 개수가 두 개 이상이면 다중선형회귀분석으로 분석
회귀분석의 변수
- 영향을 받는 변수(y)
- 반응변수(respinse variable)
- 종속변수(dependent variable)
- 결과변수(outcome variable)
- 영향을 주는 변수(x)
- 설명변수(explanatory variable)
- 독립변수(independent variable)
- 예측변수(predictor variable)
선형회귀분석의 가정
- 선형성
- 입력변수와 출력변수의 관계가 선형이다
- 등분산성
- 오차의 분산이 입력변수와 무관하게 일정하다
- 잔차플롯(산점도)를 활용하여 잔차와 입력변수간에 아무런 관련성이 없게 무작위적으로 고루 분포되어야 등분산성 가정을 만족하게 된다
- 독립성
- 입력변수와 오차는 관련이 없다
- 자기상관(독립성)을 알아보기 위해 Durbin-Wasto 통계량을 사용하며 주로 시계열 데이터에서 많이 활용한다
- 비상관성
- 오차들끼리 상관이 없다
- 정상성(정규성)
- 오차의 분포가 정규분포를 따른다
- Q-Q plot(대각방향의 직선의 형태를 지니고 있으면 됨), Kolmogolov-Smirnov검정, Shaprio-Wilk검정 등을 활용하여 정규성을 확인한다
가정에 대한 검증
- 단순선형회귀분석
- 입력변수와 출력변수간의 선형성을 점검하기 위해 산점도를 확인
- 다중선형회귀분석
- 선형회귀분석의 가정인 선형성, 등분산성, 독립성, 정상성이 모두 만족하는지 확인해야함
단순선형회귀분석
회귀분석에서의 검토사항
- 회귀계수들이 유의미한가?
- 해당 계수의 t 통계량의 p-값이 0.05보다 작으면 해당 회귀계수가 통계적으로 유익하다고 볼 수 있다
- 모형이 얼마나 설명력을 갖는가?
- 결정계수($R^2$)를 확인한다.
- 결정계수는 0~1값을 가지며, 높은 값을 가질수록 추정된 회귀식의 설명력이 높다
- 모형이 데이터를 잘 적합하고 있는가?
- 잔차를 그래프로 그리고 회귀진단을 한다
회귀계수의 추정(최소제곱법, 최소자승법)
- 측정값을 기초로 하여 적당한 제곱합을 만들고 그것을 최소로 하는 값을 구하여 측정결과를 처리하는 방법
- 잔차제곱이 가장 작은 선을 구하는 것을 의미한다
회귀분석의 검정
- 회귀계수의 검정
- 회귀계수 $\beta_i$ 이 0이면 입력변수 x와 출력변수 y사이에는 아무런 인과관계가 없다
- 회귀계수 $\beta_i$ 이 0이면 적합된 추정식은 아무 의미가 없게 된다(귀무가설 $\beta_i$ = 0, 대립가설 $\beta_i$ ≠ 0)
> x <- c(19, 23, 26, 29, 30, 38, 39, 46,49)
> y <- c(33, 51, 40, 49 ,50, 69, 70, 64, 89)
> lm(y~x)
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
6.409 1.529
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-12.766 -2.470 -1.764 4.470 9.412
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.4095 8.9272 0.718 0.496033
x 1.5295 0.2578 5.932 0.000581 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.542 on 7 degrees of freedom
Multiple R-squared: 0.8341, Adjusted R-squared: 0.8104
F-statistic: 35.19 on 1 and 7 DF, p-value: 0.0005805
- x의 회귀계수인 t통계량에 대한 p-값이 0.000581로 나타나, 유의수준인 0.05보다 작으므로 회귀계수의 추정치들이 통계적으로 유의하다
- 결정계수는 0.8341로 높게 나타나 이 회귀식이 데이터를 적절하게 설명하고 있다고는 할 수 있다
- y = 6.4095 + 1.5295 * x
- 결정계수
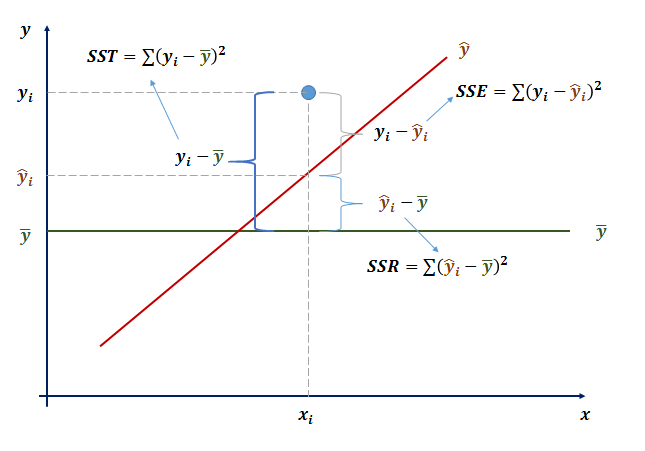
- 전체제곱합(SST)
- 회귀제곱합(SSR)
- 오차제곱합(SSE)
- 결정계수는 전체제곱합에서 회귀제곱합의 비율(SSR/SST)
- 결정계수는 전체 데이터를 회귀모형이 설명할 수 있는 설명력을 의미
- 회귀직선의 적합도 검토
- 결정계수를 통해 추정된 회귀식이 얼마나 타당한지 검토한다(결정계수가 1에 가까울수록 회귀모형이 자료를 잘 설명함)
- 독립변수가 종속변수 변동의 몇 %를 설명하는지 나타내는 지표이다
- 다변량 회귀분석에서는 독립변수의 수가 많아지면 결정계수가 높아지므로 독립변수가 유의하든, 유의하지 않든 독립변수의 수가 많아지면 결정계수가 높아지는 단점이 있다
- 이러한 결정계수의 단점을 보완하기 위해 수정된 결정계수를 활용한다, 수정된 결정계수는 결정계수보다 작은 값으로 산출되는 특징이 있다
- 오차와 잔차의 차이
- 오차: 모집단에서 실제값이 회귀선과 비교해 볼 때 나타나는 차이(정확치와 관측치의 차이)
- 잔차: 표본에서 나온 관측값이 회귀선과 비교해볼 때 나타나는 차이
다중선형회귀분석
다중선형회귀분석(다변량회귀분석)
-
다중회귀식
$Y = \beta_0 + \beta_1X_1$ + \beta_2X_2$ + … + \beta_kX_k + ε $ - 모형의 통계적 유의성
- 모형의 통계적 유의성은 F통계량으로 확인함
- 유의수준 5% 하에서 F통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다고 볼 수 있다
- F통계량이 크면 p-value가 0.05보다 작아지고 귀무가설을 기각한다, 모형이 유의하다고 결론지을 수 있다
- 회귀계수의 유의성
- 회귀계수의 유의성은 단변량 회귀분석의 회귀계수 유의성 검토와 같이 t통계량을 통해 확인
- 모든 회귀계수의 유의성이 통계적으로 검증되어야 선택된 변수들의 조합으로 모형을 활용할 수 있음
- 모형의 설명력
- 결정계수나 수정된 결정계수를 확인한다
- 모형의 적합성
- 모형이 데이터를 잘 적합하고 있는지 잔차와 종속변수의 산점도로 확인한다
- 데이터가 전제하는 가정을 만족시키시는가?
- 선형성, 독립성, 등분산성, 비상관성, 정상성
- 다중공산성(multicollinearity)
- 다중회귀분석에서 설명변수들 사이에 선형관계가 존재하면 회귀계수의 정확한 추정이 곤란
- 다중공산성 검사 방법
- 분산팽창요인(VIF): 4보다 크면 다중공산성이 존재한다고 볼 수 있고, 10보다 크면 심각한 문제가 있는 것으로 해석
- 상태지수: 10 이상이면 문제가 있다고 보고, 30보다 크면 심각한 문제가 있다고 해석할 수 있다
- 다중선형회귀분석에서 다중공산성의 문제가 발생하면, 문제가 있는 변수를 제거하거나 주성분회귀, 능형회귀 모형을 적용하여 문제를 해결한다
회귀분석의 종류
- 단순회귀
- 독립변수가 1개이며 종속변수와의 관계가 직선
- 다중회귀
- 독립변수가 k개이며 종속변수와의 관계가 선형(1차함수)
- 로지스틱 회귀
- 종속변수가 범주형(2진변수)인 경우에 적용되며, 단순 로지스틱 회귀 및 다중, 다항 로지스틱 회귀로 확장할 수 있음
- 다항회귀
- 독립변수와 종속변수와의 관계가 1차 함수이상인 관계(단, k=1이면 2차 함수 이상)
- 곡선회귀
- 독립변수가 1개이며 종속변수와의 관계가 곡선
- 비선형회귀
- 회귀식의 모양이 미지의 모수들의 선형관계로 이뤄져 있지 않은 모형
회귀분석 사례
회귀분석 사례
> library(MASS)
> head(Cars37)
Error in head(Cars37) : object 'Cars37' not found
> head(Cars97)
Error in head(Cars97) : object 'Cars97' not found
> library(MASS)
> head(Cars93)
Manufacturer Model Type Min.Price Price Max.Price MPG.city MPG.highway AirBags DriveTrain Cylinders EngineSize
1 Acura Integra Small 12.9 15.9 18.8 25 31 None Front 4 1.8
2 Acura Legend Midsize 29.2 33.9 38.7 18 25 Driver & Passenger Front 6 3.2
3 Audi 90 Compact 25.9 29.1 32.3 20 26 Driver only Front 6 2.8
4 Audi 100 Midsize 30.8 37.7 44.6 19 26 Driver & Passenger Front 6 2.8
5 BMW 535i Midsize 23.7 30.0 36.2 22 30 Driver only Rear 4 3.5
6 Buick Century Midsize 14.2 15.7 17.3 22 31 Driver only Front 4 2.2
Horsepower RPM Rev.per.mile Man.trans.avail Fuel.tank.capacity Passengers Length Wheelbase Width Turn.circle Rear.seat.room
1 140 6300 2890 Yes 13.2 5 177 102 68 37 26.5
2 200 5500 2335 Yes 18.0 5 195 115 71 38 30.0
3 172 5500 2280 Yes 16.9 5 180 102 67 37 28.0
4 172 5500 2535 Yes 21.1 6 193 106 70 37 31.0
5 208 5700 2545 Yes 21.1 4 186 109 69 39 27.0
6 110 5200 2565 No 16.4 6 189 105 69 41 28.0
Luggage.room Weight Origin Make
1 11 2705 non-USA Acura Integra
2 15 3560 non-USA Acura Legend
3 14 3375 non-USA Audi 90
4 17 3405 non-USA Audi 100
5 13 3640 non-USA BMW 535i
6 16 2880 USA Buick Century
> attach(Cars93)
> lm(Price~EngineSize+RPM+Weight, data = Cars93)
Call:
lm(formula = Price ~ EngineSize + RPM + Weight, data = Cars93)
Coefficients:
(Intercept) EngineSize RPM Weight
-51.793292 4.305387 0.007096 0.007271
> summary(lm(Price~EngineSize+RPM+Weight, data = Cars93))
Call:
lm(formula = Price ~ EngineSize + RPM + Weight, data = Cars93)
Residuals:
Min 1Q Median 3Q Max
-10.511 -3.806 -0.300 1.447 35.255
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -51.793292 9.106309 -5.688 1.62e-07 ***
EngineSize 4.305387 1.324961 3.249 0.00163 **
RPM 0.007096 0.001363 5.208 1.22e-06 ***
Weight 0.007271 0.002157 3.372 0.00111 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.504 on 89 degrees of freedom
Multiple R-squared: 0.5614, Adjusted R-squared: 0.5467
F-statistic: 37.98 on 3 and 89 DF, p-value: 6.746e-16
- 여기서 F통계량은 37.98이며 유의확률 p-value 값이 6.746e-16로 유의수준 5%하에서 추정된 회귀 모형이 통계적으로 매우 유의함을 알 수 있다
- 결정계수와 수정된 결정계수는 각각 0.5614, 0.5467로 조금 낮게 나타나 이 회귀식이 데이터를 적절하게 설명하고 있다고는 할 수 없다
- 회귀계수들의 p-값들이 0.05보다 작으므로 회귀계수의 추정치들이 통계적으로 유의하다
- 결정계수가 낮아 데이터의 설명력은 낮지만 회귀분석 결과에서 회귀식과 회귀계수들이 통계적으로 유의하여 자동차의 가격을 엔진의 크기와 RPM 그리고 무게로 추정할 수 있다
로지스틱 회귀분석 사례
> library(boot)
> data(nodal)
> a <- c(2,4,6,7)
> data <- nodal[,a]
> glmModel <- glm(r~., data=data, family = "binomial")
> summary(glmModel)
Call:
glm(formula = r ~ ., family = "binomial", data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1231 -0.6620 -0.3039 0.4710 2.4892
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.0518 0.8420 -3.624 0.00029 ***
stage 1.6453 0.7297 2.255 0.02414 *
xray 1.9116 0.7771 2.460 0.01390 *
acid 1.6378 0.7539 2.172 0.02983 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 70.252 on 52 degrees of freedom
Residual deviance: 49.180 on 49 degrees of freedom
AIC: 57.18
Number of Fisher Scoring iterations: 5
- 2번째 변수인 양성여부를 종속변수로 두고 5개의 변수를 독립변수로 하여 로지스틱 회귀분석을 실시한 결과 age와 grade는 유의수준 5%하에서 유의하지 않아 이를 제외한 3개 변수 stage, xray와 acid를 활용해서 모형을 개발한다
- stage, xray와 acid의 추정계수는 유의수준 5% 하에서 유의하게 나타나므로 p(r=1)=1/(1+e-3.05+1.65stage+1.91xray+1.64acid)의 선형식 가능
최적회귀방정식
최적회귀방정식의 선택
- 설명변수
- 필요한 변수만 상황에 따라 타협을 통해 선택
- y에 영향을 미칠 수 있는 모든 설명변수 x들을 y의 값을 예측하는데 참여
- 데이터에 설명변수 x들의 수가 많아지면 관리하는데 많은 노력이 요구되므로, 가능한 범위 내에서 적은 수의 설명변수를 포함
- 모형선택(exploratory analysis) : 분석 데이터에 가장 잘 맞는 모형을 찾아내는 방법
- 모든 가능한 조합의 회귀분석 : 모든 가능한 독립변수들의 조합에 대한 회귀모형을 생성한 뒤 가장 적합한 회귀모형을 선택
- 단계적 변수선택(Stepwise Variable Selection)
- 전진선택법(forward selection) : 절편만 있는 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
- 변수의 개수가 많은 경우에도 사용가능
- 변수값의 작은 변동에도 결과가 크게 달라져 안정성이 부족
- 후진제거법(backward elimination) : 독립변수 후보 모두를 포함한 모형에서 출발해 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 제거할 변수가 없을 때의 모형을 선택
- 전체 변수들의 정보를 이용하는 장점, 변수의 개수가 많은 경우 사용하기 어려움
- 단계선택법(stepwise method) : 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수의 중요도가 약화되면 해당변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단
- 전진선택법(forward selection) : 절편만 있는 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
벌점화된 선택기준
- 개요
- 모형의 복잡도에 벌점을 주는 방법으로 AIC 방법과 BIC 방법이 주로사용
- 설명
- 모든 후보 모형들에 대해 AIC 또는 BIC를 계산하고 그 값이 최소가 되는 모형을 선택
- 모형선택의 일치성(consistency inselection) : 자료의 수가 늘어날 때 참인 모형이 주어진 모형 선택 기준의 최소값을 갖게 되는 성질
- 이론적으로 AIC에 대해서 일치성이 성립하지 않지만 BIC는 주요 분포에서 이러한 성질이 성립
- AIC를 활용하는 방법이 보편화
- 다른방법으로는 RIC, CIC, DIC가 있음
최적회귀방정식의 사례
- 변수 선택법 예제(유의확률 기반)
> # 데이터 프레임 생성
> x1<-c(7,1,11,11,7,11,3,1,2,21,1,11,10)
> x2<-c(26,29,56,31,52,55,71,31,54,47,40,66,68)
> x3<-c(6,15,8,8,6,9,17,22,18,4,23,9,8)
> x4<-c(60,52,20,47,33,22,6,44,22,26,34,12,12)
> y<-c(78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3,109.4)
> df <- data.frame(x1,x2,x3,x4,y)
> head(df)
x1 x2 x3 x4 y
1 7 26 6 60 78.5
2 1 29 15 52 74.3
3 11 56 8 20 104.3
4 11 31 8 47 87.6
5 7 52 6 33 95.9
6 11 55 9 22 109.2
> # 회귀모형(a) 생성
> a <- lm(y~x1+x2+x3+x4, data=df)
> summary(a)
Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.1750 -1.6709 0.2508 1.3783 3.9254
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.4054 70.0710 0.891 0.3991
x1 1.5511 0.7448 2.083 0.0708 .
x2 0.5102 0.7238 0.705 0.5009
x3 0.1019 0.7547 0.135 0.8959
x4 -0.1441 0.7091 -0.203 0.8441
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.446 on 8 degrees of freedom
Multiple R-squared: 0.9824, Adjusted R-squared: 0.9736
F-statistic: 111.5 on 4 and 8 DF, p-value: 4.756e-07
- F-통계량을 확인한 결과 111.5로 나타났으며 유의확률이 4.756e-07임으로 통계적으로 유의하게 나타났다
- 하지만 각각의 t 통계량을 통한 유의확률이 0.05 보다 작은 변수가 하나도 존재하지 않아 모형을 활용할 수 없다고 판단
# 유의확률이 가장 높은 변수를 제거하고 다시 회귀모형(b) 생성
> b <- lm(y~x1+x2+x4, data=df)
> summary(b)
Call:
lm(formula = y ~ x1 + x2 + x4, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.0919 -1.8016 0.2562 1.2818 3.8982
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 71.6483 14.1424 5.066 0.000675 ***
x1 1.4519 0.1170 12.410 5.78e-07 ***
x2 0.4161 0.1856 2.242 0.051687 .
x4 -0.2365 0.1733 -1.365 0.205395
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.309 on 9 degrees of freedom
Multiple R-squared: 0.9823, Adjusted R-squared: 0.9764
F-statistic: 166.8 on 3 and 9 DF, p-value: 3.323e-08
- x3 변수를 제거한 후, 모형의 유의성을 다시 검토한 결과 F 통계량에 대한 유의확률은 통계적으로 유의하게 나타났음
- 모든 변수들이 t 통계량에 대한 유의확률이 0.05보다 낮아야하지만 x1을 제외한 2개 변수의 유의확률이 0.05보다 높게 나타나 유의하지 않는 결과를 보임
- 유의확률이 가장 높은 x4를 제외하고 회귀모형을 다시 생성
> c <- lm(y ~ x1+x2, data = df)
> summary(c)
Call:
lm(formula = y ~ x1 + x2, data = df)
Residuals:
Min 1Q Median 3Q Max
-2.893 -1.574 -1.302 1.363 4.048
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.57735 2.28617 23.00 5.46e-10 ***
x1 1.46831 0.12130 12.11 2.69e-07 ***
x2 0.66225 0.04585 14.44 5.03e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.406 on 10 degrees of freedom
Multiple R-squared: 0.9787, Adjusted R-squared: 0.9744
F-statistic: 229.5 on 2 and 10 DF, p-value: 4.407e-09
- F통계량을 통해 유의수준 0.05하에서 모형이 통계적으로 유의
- 수정된 결정계수는 0.9744로 선정된 다변량회귀식이 전체 데이터의 97.44%를 설명하고 있는 것을 확인할 수 있음
- 후진제거법을 통해 최종적으로 얻게된 추정된 회귀식은 y = 52.57735 + 1.46831x1 + 0.66225x2
- 변수 선택법 예제(벌점화 전진선택법)
- step함수를 이용하여 전진선택법을 적용
- step(lm(출력변수~입력변수, 데이터세트), scope=list(lower=~1, upper=~입력변수), direction=”변수선택방법”)
- scope - 변수선택과정에서 설정할 수 있는 가장 큰 모형 혹은 작은 모형을 설정, scope가 없을 경우 전진선택법에서는 현재 선택한 모형을 가장 큰 모형으로, 후진제거법에서는 상수항만 있는 모형을 가장 작은 모형으로 설정
- direction - 변수선택법(forward: 전진선택법, backward: 후진제거법, stepwise: 딘계적선택법)
- k - 모형선택 기준에서 AIC, BIC와 같은 옵션을 사용 - k=2이면 AIC, k=log(자료의 수)이면 BIC
> # step함수를 이용한 전진선택법의 적용
> step(lm(y~1, data=df), scope = list(lower=~1, upper=~x1+x2+x3+x4), direction="forward")
Start: AIC=71.44
y ~ 1
Df Sum of Sq RSS AIC
+ x4 1 1831.90 883.87 58.852
+ x2 1 1809.43 906.34 59.178
+ x1 1 1450.08 1265.69 63.519
+ x3 1 776.36 1939.40 69.067
<none> 2715.76 71.444
Step: AIC=58.85
y ~ x4
Df Sum of Sq RSS AIC
+ x1 1 809.10 74.76 28.742
+ x3 1 708.13 175.74 39.853
<none> 883.87 58.852
+ x2 1 14.99 868.88 60.629
Step: AIC=28.74
y ~ x4 + x1
Df Sum of Sq RSS AIC
+ x2 1 26.789 47.973 24.974
+ x3 1 23.926 50.836 25.728
<none> 74.762 28.742
Step: AIC=24.97
y ~ x4 + x1 + x2
Df Sum of Sq RSS AIC
<none> 47.973 24.974
+ x3 1 0.10909 47.864 26.944
Call:
lm(formula = y ~ x4 + x1 + x2, data = df)
Coefficients:
(Intercept) x4 x1 x2
71.6483 -0.2365 1.4519 0.4161
- 벌점화 방식을 적용한 전진선택법을 실시한 결과, 가장먼저 선택된 변수는 AIC값이 58.852으로 가장낮은 x4였다. x4에 x1을 추가하였을때 AIC 값이 28.742로 낮아지게 되었고, x2를 추가하였을때 AIC값이 24.974로 최소화되어 더 이상 AIC를 낮출 수 없어 변수선택을 종료하게 되었다.
- 최종적으로 선택된 추정된 회귀식은 y = 71.6483 - 0.2365x4 + 1.4519x1 +0.4161x2
- 변수 선택법 예제(벌점화 후진선택법)
library(ElemStatLearn)
Data=prostate
data.use = Data[,-ncol(Data)]
lm.full.Model = lm(lpsa~., data=data.use)
backward.aic = step(lm.full.Model, lpsa~1, direction = "backward")
시계열 분석
시계열 자료
- 시간의 흐름에 따라 관찰된 값들을 시계열 자료라 한다
- 시계열 자료의 종류
- 비정상성 시계열 자료
- 시계열 분석을 실시할 때 다루기 어려운 자료로 대부분의 시계열자료가 이에 해당
- 정상성 시계열 자료
- 비정상 시계열 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료
- 비정상성 시계열 자료
정상성
- 평균이 일정한 경우
- 모든 시점에 대해 일정한 평균을 가짐
- 평균이 일정하지 않은 시계열은 차분(differnece)을 통해 정상화할 수 있음
- 차분 : 현시점 자료에서 전 시점 자료를 빼는 것
- 일반차분(regular differnece) : 바로 전 시점의 자료를 빼는 방법
- 계절차분(seasonal difference) : 여러 시점 전의 자료를 빼는 법, 계절성을 갖는 자료를 정상화하는데 사용
- 분산이 일정
- 분산도 시점에 의존하지 않고 일정
- 분산이 일정하지 않을 경우 변환(Transformation)을 통해 정상화
- 공분산도 단지 시차에만 의존, 실제 특정 시점 t, s에는 의존하지 않음
- 정상 시계열의 특징
- 정상 시계열은 어떤 시점에서 평균과 분산 그리고 특정한 시차의 길이를 갖는 자기공분산을 측정하더라도 동일한 값을 갖음
- 정상 시계열은 항상 그 평균값으로 회귀하려는 경향이 있으며, 그 평균값 주변에서의 변동은 대체로 일정한 폭을 갖음
- 정상 시계열이 아닌 경우 특정 기간의 시계열 자료로부터 얻은 정보를 다른 시기로 일반화 할 수 없음
시계열자료 분석방법
분석방법
- 회귀분석방법, Box-Jenkins 방법, 지수평활법, 시계열 분해법 등
수학적 이론모형: 회귀분석(계량경제)방법, Box-Jenkins 방법
직관적 방법: 지수평활법, 시계열 분해법으로 시간에 따른 변동이 느린 데이터 분석에 활용
장기 예측: 회귀분석방법 활용
단기 예측: Box-Jenkins 방법, 지수평활법, 시계열 분해법 활용
자료 형태에 따른 분석방법
- 일변량 시계열분석
- Box-Jenkins(ARMA), 지수 평활법, 시계열 분해법 등
- 시간을 설명변수로 한 회귀모형주가, 소매물가지수 등 하나의 변수에 관심을 갖는 경우의 시계열분석
- 다중 시계열분석
- 계량경제 모형, 전이함수 모형, 개입분석, 상태공간 분석, 다변량 ARIMA
- 계량경제: 시계열 데이터에 대한 회귀분석(예: 이자율, 인플레이션이 환율에 미치는 요인)
- 여러개의 시간(t)에 따른 변수들을 활용하는 시계열 분석
이동평균법
- 계량경제 모형, 전이함수 모형, 개입분석, 상태공간 분석, 다변량 ARIMA
- 이동평균법의 개념
- 과거로부터 현재까지의 시계열 자료를 대상으로 일정기간별 이동평균을 계산하고, 이들의 추세를 파악하여 다음 기간을 예측하는 방법
- 시계열 자료에서 계절변동과 불규칙변동을 제거하여 추세변동과 순환변동만 가진 시계열로 변환하는 방법으로 사용
- n개의 시계열 데이터를 m기간으로 이동평균하면 n-m+1개의 이동평균 데이터가 생성
- 이동평균법의 특징
- 간단하고 쉽게 미래를 예측할 수 있으며, 자료의 수가 많고 안정된 패턴을 보이는 경우 예측의 품질이 높음
- 특정 기간 안에 속하는 시계열에 대해서는 동일한 가중치를 부여
- 일반적으로 시계열 자료에 뚜렷한 추세가 있거나 불규칙변동이 심하지 않은 경우에는 짧은기간의 평균을 사용, 반대로 불규칙변동이 심한 경우 긴 기간의 평균을 사용
- 이동평균법에서 가장 중요한 것은 적절한 시간을 사용하는 것, 즉, 적절한n의 개수를 설정하는 것
지수평활법
- 지수평활법의 개념
- 일정기간의 평균을 이용하는 이동평균법과 달리 모든 시계열 자료를 사용하여 평균을 구하며, 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래를 예측하는 방법
- 지수평활법의 특징
- 단기간에 발생하는 불규칙변동을 평활하는 방법
- 자료의 수가 많고, 안정된 패턴을 보이는 경우일수록 예측 품질이 높음
- 지수평활법에서 가중치 역할을 하는것은 지수평활계수($\alpha$)이며, 불규칙변동이 큰 시계열의 경우 지수평활계수는 작은 값을, 불규칙변동이 작은 시계열의 경우, 큰 값의 지수평활계수를 적용
- 지수평활계수는 예측오차를 비교하여 예측오차가 가장 작은 값을 선택하는 것이 바람직함
- 지수평활계수는 과거로 갈수록 지속적으로 감소함
- 지수평활법은 불규칙변동의 영향을 제거하는 효과가 있으며, 중기 예측 이상에 주로 사용(단, 단순지수 평활법의 경우 장기추세나 계절변동이 포함된 시계열의 예측에는 적합하지 않음)
시계열모형
자기회귀 모형(AR 모형)
p 시점 전의 자료가 현재 자료에 영향을 주는 모형
- AR(1)모형 : 직전 시점 데이터로만 분석
- AR(2)모형 : 연속된 2시점 정도의 데이터로 분석
- 자기상관함수(ACF, k기간 떨어진 값들 $log(k)$의 상관계수를 함수 형태로 표시한 것)는 빠르게 감소, 부분자기함수(PACF, 두시점 사이의 관계를 분석할 때 중간에 있는 값들의 영향을 제외시킨 상관관계 개념)는 어느 시점에서 절단점을 가짐
- ACF가 빠르게 감소하고, PACF가 3시점에서 절단점을 갖는 그래프가 있다면, 2시점 전의 자료까지가 현재에 영향을 미치는 AR(2) 모형이라 볼 수 있음
이동평균모형(MA 모형)
- 유한한 개수의 백색잡음의 결합, 정상성 만족
- 1차 이동평균모형(MA1 모형)은 이동평균모형 중에서 가장 간단한 모형으로 시계열이 같은 시점의 백색잡음과 바로 전 시점의 백색잡음의 결합으로 이뤄진 모형
- 2차 이동평균모형(MA2 모형)은 바로 전 시점의 백색잡음과 시차가 2인 백색잡음의 결합으로 이뤄진 모형
- AR 모형과 반대로 ACF에서 절단점을 갖고, PACF가 빠르게 감소
자기회귀누적이동평균 모형(ARIMA(p,d,q)모형)
- ARIMA 모형은 비정상시계열 모형
- ARIMA 모형을 차분이나 변환을 통해 AR모형이나 MA모형, 이 둘을 합친 ARMA 모형으로 정상화할 수 있음
- p는 AR 모형, q는 MA모형과 관련이 있는 차수이다
- 시계열 {$Z_t$}의 d번 차분한 시계열이 ARMA(p,q) 모형이면, 시계열 {$Z_t$}는 차수가 p,d,q인 ARIMA 모형, 즉 ARIMA(p,d,q) 모형을 갖는다고 한다
- d=0이면 ARMA(p,q) 모형이라 부르고, 이모형은 정상성 만족(ARMA(0,0)일경우 정상화가 불필요)
- p=0이면 IMA(d,q) 모형이라고 부르고, d번 차분하면 MA(q)모형을 따름
- q=0이면 ARI(p,d) 모형이라고 부르며, d번 차분한 시계열이 AR(p)모형을 따름
- 예시
- ARIMA(0,1,1) -> 1차분 후 MA(1)
- ARIMA(1,1,0) -> 1차분 후 ARI(1)
- ARIMA(1,1,2) -> 1차분 후 AR(1), MA(2), ARMA(1,2) 선택 활용
- 이런 경우 가장 간단한 모형을 선택하거나 AIC를 적용하여 점수가 가장 낮은 모형 선정
분해 시계열
- 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석, 회귀분석적인 방법을 주로 사용
R을 이용한 시계열분석 예시
분해 시계열
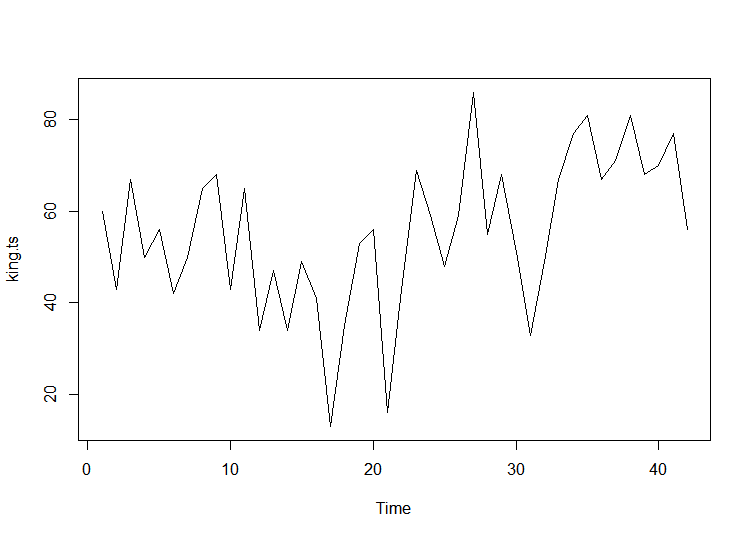
#자료읽기 및 그래프그리기
king <- scan("http://robjhyndman.com/tsdldata/misc/kings.dat",skip=3)
king.ts <- ts(king)
plot.ts(king.ts)
# 3년마다 평균을 내서 그래프를 부드럽게 표현
king.sma3 <- SMA(king.ts, n=3)
plot.ts(king.sma3)
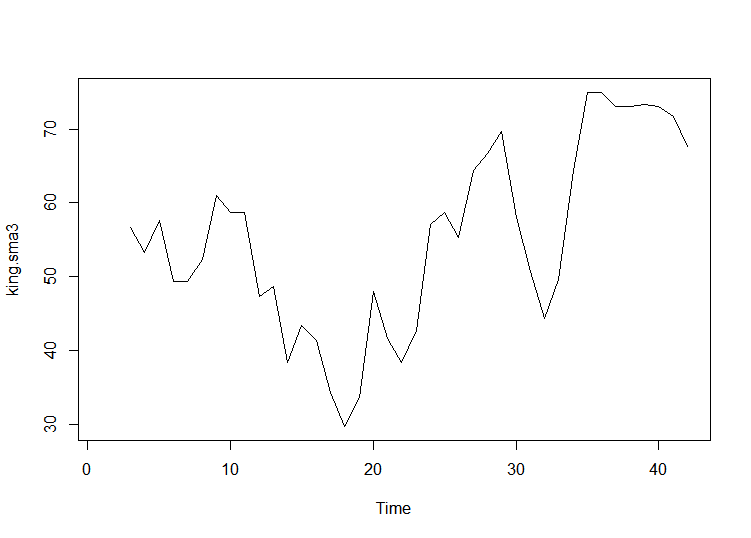
ARIMA 모델
- ARIMA 모델은 정상성 시계열에 한해 사용
- 비정상 시계열 자료는 차분해 정상성으로 만족하는 조건의 시계열로 바꿔줌
- 위에서 본 데이터에서 평균이 시간에 따라 일정하지 않은 모습을 보이므로 비정상시계열임 -> 차분진행
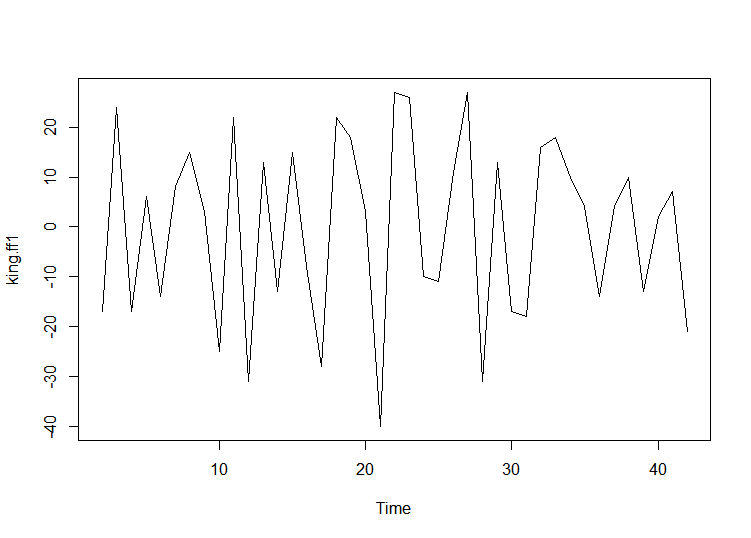
- 1차차분결과에서 평균과 분산이 시간에 따라 의존하지 않음을 확인
- ARIMA(p,1,q) 모델이며 차분을 1번해야 정상성을 만족
# 차분하기
king.ff1 <- diff(king.ts, differences =1)
plot.ts(king.ff1)
- ACF와 PACF를 통한 적합한 ARIMA 모델 결정
- ACF
- lag는 0부터 값을 갖는데, 너무 많은 구간을 설정하면 그래프보고 판단하기 어려움
- ACF 값이 lag 1인 지점 빼고는 모두 점선 구간 안에 있고, 나머지는 구간 안에 있음
> #ACF
> acf(king.ff1, lag.max = 20)
> acf(king.ff1, lag.max = 20, plot = FALSE)
Autocorrelations of series ‘king.ff1’, by lag
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
1.000 -0.360 -0.162 -0.050 0.227 -0.042 -0.181 0.095 0.064 -0.116 -0.071 0.206 -0.017 -0.212 0.130 0.114 -0.009 -0.192 0.072
19 20
0.113 -0.093
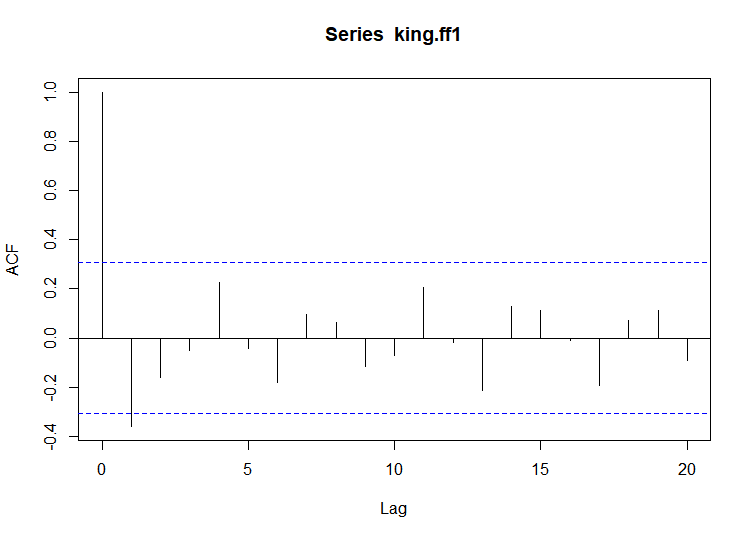
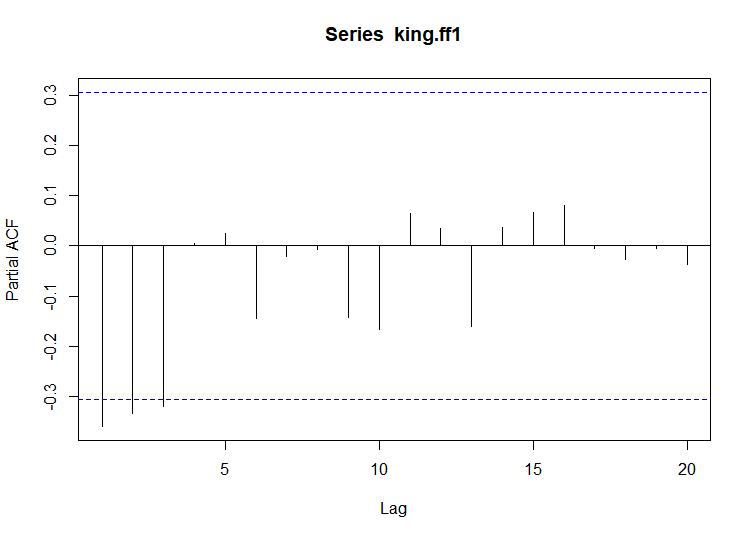
- PACF - PACF 값이 lag 1,2,3에서 점선 구간을 초과하고 음의 값을 가지며 절단점이 lag 4
> # pacf
> pacf(king.ff1, lag.max = 20)
> pacf(king.ff1, lag.max = 20, plot = FALSE)
Partial autocorrelations of series ‘king.ff1’, by lag
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
-0.360 -0.335 -0.321 0.005 0.025 -0.144 -0.022 -0.007 -0.143 -0.167 0.065 0.034 -0.161 0.036 0.066 0.081 -0.005 -0.027 -0.006
20
-0.037
종합
- ARMA 후보 생성
- ARMA(3,0) 모델: PACF 값이 lag4에서 절단점을 가짐. AR(3) 모형
- ARMA(0,1) 모델: ACF 값이 lag2에서 절단점을 가짐. MA(1)모형
- ARMA(p,q) 모델: 그래서 AR모형과 MA모형을 혼합
적절한 ARIMA 모형 찾기
- forecast package에 내장된 auto.arima()함수 이용
- 아래 결과로 보아 적절한 ARIMA모형은 ARIMA(0,1,1)임
```r
#적절한 ARIMA모형 auto.arima(king) Series: king ARIMA(0,1,1)
Coefficients: ma1 -0.7218 s.e. 0.1208
sigma^2 estimated as 236.2: log likelihood=-170.06 AIC=344.13 AICc=344.44 BIC=347.56
#### 예측
```r
> #예측
> king.arima <- arima(king, order = c(0,1,1))
> king.forecasts <- forecast(king.arima)
> king.forecasts
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
43 67.75063 48.29647 87.20479 37.99806 97.50319
44 67.75063 47.55748 87.94377 36.86788 98.63338
45 67.75063 46.84460 88.65665 35.77762 99.72363
46 67.75063 46.15524 89.34601 34.72333 100.77792
47 67.75063 45.48722 90.01404 33.70168 101.79958
48 67.75063 44.83866 90.66260 32.70979 102.79146
49 67.75063 44.20796 91.29330 31.74523 103.75603
50 67.75063 43.59372 91.90753 30.80583 104.69543
51 67.75063 42.99472 92.50653 29.88974 105.61152
52 67.75063 42.40988 93.09138 28.99529 106.50596
- 42명의 영국 왕 중에서 마지막 왕의 사망시 나이는 56세
- 43번째에서 52번째 왕까지 10명의 왕의 사망시 나이를 예측한 결과 67.75살로 추정
- 5명정도만 예측하고 싶을시, 옵션에 h=5
- 신뢰구간은 80%~95% 사이

댓글남기기