[ADSP] 3과목 4장 통계분석 -3
다차원척도법
다차원척도법(MUltidimensional Scaling)
- 객체간 근접성(Proximity)을 시각화하는 통계기법
- 군집분석과 같이 개체들을 대상으로 변수들을 측정한 후 개체들 사이의 유사성/비유사성을 측정하여 개체들을 2차원 공간상에 점으로 표현하는 분석방법
- 개체들을 2차원 또는 3차원 공간상에 점으로 표현하여 개체들 사이의 집단화를 시각적으로 표현
다차원척도법 목적
- 데이터 속에 잠재해 있는 패턴(pattern), 구조를 찾아낸다
- 그 구조를 소수 차원의 공간에 기하학적으로 표현한다
- 데이터 축소(Data Reduction)의 목적으로 다차원척도법을 이용한다
- 데이터에 포함되는 정보를 끄집어내기 위해서 다차원척도법을 탐색수단으로 사용
- 다차원척도법에 의해서 얻은 결과를, 데이터가 만들어진 현상이나 과정에 고유의 구조로서 의미를 부여한다
다차원척도법 방법
- 개체들의 거리 계산에는 유클리드 거리행렬 활용
- 관측대상들의 상대적 거리의 정확도를 높이기 위해 적합 정도를 스트레스 값(Stress Value)로 나타냄
- 각 개체들을 공간상에 표현하기 위한 방법은 부적합도 기준으로 STRESS나 S-STRESS를 사용
- 최적모형의 적합은 부적합도를 최소로하는 반복알고리즘 이용
- STRESS 적합도 수준 M은 개체들을 공간상에 표현하기 위한 방법으로 STRESS나 S-STRESS를 부적합도 기준으로 사용
- 최적모형의 적합은 부적합도를 최소로 하는 방법으로 일정 수준이하로 될 때까지 반복해서 수행
| STRESS | 적합도 수준 |
|---|---|
| 0 | 완벽 |
| 0.05 이내 | 매우 좋은 |
| 0.05~0.10 | 만족 |
| 0.10~0.15 | 보통 |
| 0.15 이상 | 나쁨 |
다차원척도법 종류
- 계량적 MDS(Metric MDS)
- 데이터가 구간척도나 비율척도인 경우 활용
- N개의 케이스에 대해서 p개의 특성변수가 있는 경우, 각 개체들간의 유클리드 거리행렬을 계산하고 개체들간의 비유사성을 공간상에 표현
아래는 cmdscale 사례이다.
library(MASS)
loc <- cmdscale(eurodist)
x<-loc[,1]
y<--loc[,2]
plot(x,y,type="n",asp=1,main="Metric MDS")
text(x,y,rownames(loc),cex=0.7)
abline(v=0,h=0,lty=2,lwd=0.5)
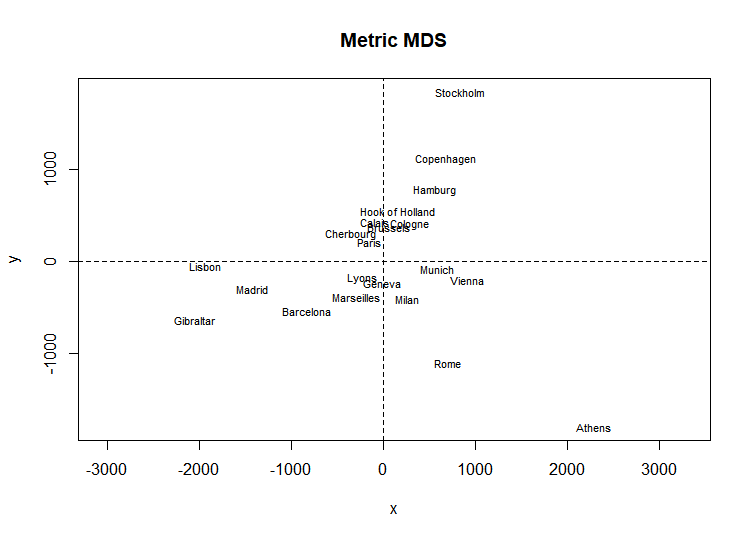
- 비계량적 MDS(nonmetric MDS)
- 데이터가 순서척도인 경우 활용
- 개체들간의 거리가 순서로 주어진 경우에는 순서척도를 거리의 속성과 같도록 변환하여 거리를 생성한 후 적용
아래는 isoMDS 사례이다.
library(MASS)
data(swiss)
swiss.x <- as.matrix(swiss[,-1]) # 1행빼고 넣기
swiss.dist <- dist(swiss.x) # dist는 행간 거리 구하기
swiss.mds <- isoMDS(swiss.dist)
plot(swiss.mds$points, type = "n")
text(swiss.mds$points, labels = as.character(1:nrow(swiss.x)))
abline(v=0,h=0,lty=2,lwd=0.5)
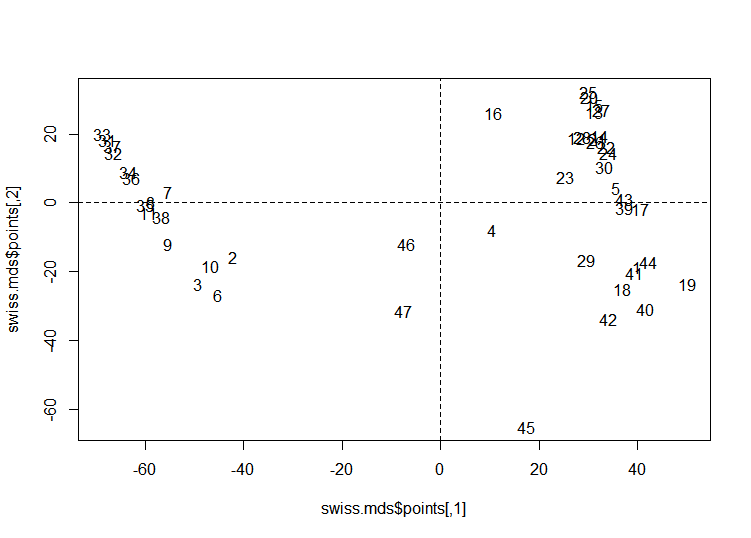
아래는 sammon 사례이다.
swiss.x <- as.matrix(swiss[,-1])
swiss.sammon <- sammon(dist(swiss.x))
plot(swiss.sammon$points, type = "n")
text(swiss.sammon$points, labels=as.character(1:nrow(swiss.x)))
abline(v=0, h=0, lty=2, lwd=0.5)
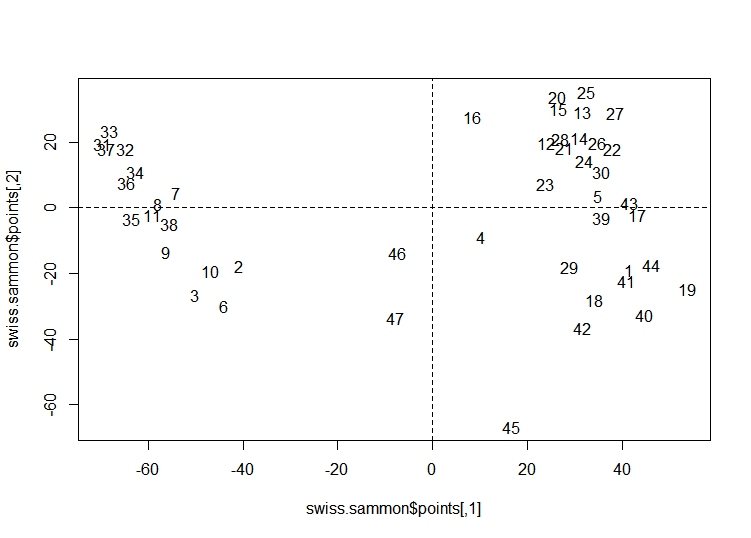
주성분 분석
주성분분석(Principal Component Analysis)
- 여러 변수의 변량을 ‘주성분’이라는 서로 상관성이 높은 변수들의 선형 결합으로 만들어 기존의 상관성이 높은 변수들을 요약, 축소하는 기법
- 첫 번째 주성분으로 전체 변동을 가장 많이 설명할 수 있도록 하고, 두 번째 주성분으로는 첫 번째 주성분과는 상관성이 없어서 첫 번째 주성분이 설명하지 못하는 나머지 변동을 정보의 손실 없이 가장 많이 설명할 수 있도록 변수들의 선형조합 만듬
주성분분석의 목적
- 여러 변수들 간에 내재하는 상관관계, 연관성을 이용해 소수의 주성분으로 차원을 축소하여 데이터를 이해하기 쉽고 관리하기 쉽게해준다
- 다중공선성이 존재하는 경우, 상관성이 없는(적은) 주성분으로 변수들을 축소하여 모형 개발에 활용
- 회귀분석 등의 모형 개발시 입력변수들간의 상관관계가 높은 다중공선성(multicollinearity)이 존재할 경우 모형이 잘못 만들어짐
- 연관성이 높은 변수를 주성분분석을 통해 차원 축소 후 군집분석을 수행하면 군집화 결과와 연산속도 개선
- 다수의 센서데이터를 주성분분석으로 차원을 축소한 후에 시계열로 분포나 추세의 변화를 분석하면 기계의 고장 징후를 사전에 파악하는데 활용
주성분분석 vs 요인분석
- 요인분석(Factor Analysis)
- 등간척도(혹은 비율척도)로 측정한 두 개 이상의 변수들에 잠재되어 있는 공통인자를 찾아내는 기법
- 공통점
- 모두 데이터를 축소하는데 활용
- 원래 데이터를 활용해서 몇 개의 새로운 변수들을 만들 수 있음
- 차이점
- 생성된 변수의 수
- 요인분석은 몇 개라고 지정 없이 만들 수 있다.
- 주성분분석은 제1주성분, 제2주성분, 제3주성분 정도로 활용
- 생성된 변수의 이름
- 요인분석은 분석자가 요인의 이름을 명명
- 주성분분석은 제1주성분, 제2주성분 등으로 표현
- 생성된 변수들 간의 관계
- 요인분석은 새 변수들은 기본적으로 대등한관계, ‘어떤 것이 더 중요하다’라는 의미없음. 단, 분류/예측 다음 단계로 사용된다면 그 때 중요성의 의미가 부여
- 주성분분석은 제1주성분이 가장 중요하고, 그 다음 제2주성분이 중요하게 취급
- 분석 방법의 의미
- 요인분석은 목표변수를 고려하지 않고 그냥 데이터가 주어지면 변수들을 비슷한 성격들로 묶어서 새로운 [잠재]변수들을 만듬
- 주성분분석은 목표 변수를 고려하여 목표 변수를 잘 예측/분류하기 위하여 원래 변수들의 선형 결합으로 이루어진 몇 개의 주성분(변수)들을 찾아내게 됨
- 생성된 변수의 수
주성분의 선택법
- 주성분분석 결과에서 누적기여율(cumulative proportion)이 85%이상이면 주성분의 수로 결정할 수 있다
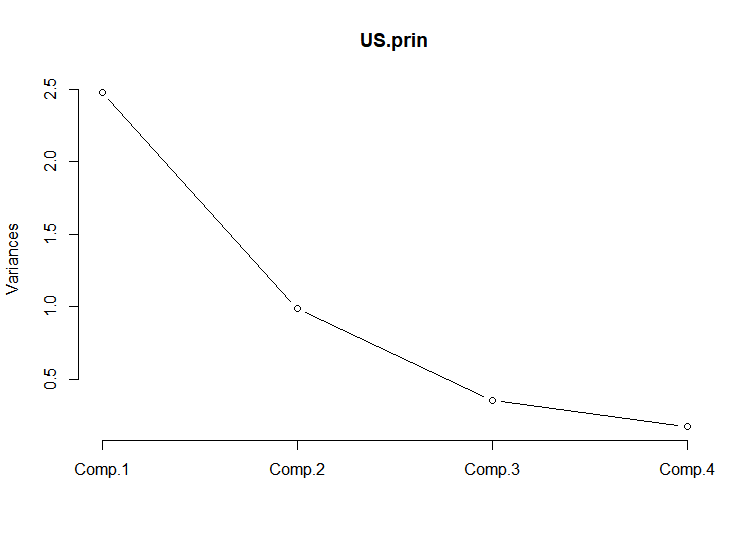
- scree plot을 활용하여 고유값(eigenvalue)이 수평을 유지하기 전단계로 주성분의 수를 선택한다
주성분 분석 사례
USArrests 자료
- 1973년 미국 50개주의 100,000명의 인구 당 체포된 세 가지 강력범죄수(assault, murder, rape)와 각 주마다 도시에 거주하는 인구의 비율(%)로 구성
- 변수들 간의 척도의 차이가 상단히 크기 때문에 상관행렬을 사용하여 분석
- 특이치 분해를 사용하는 경우 자료 행렬의 각 변수의 평균과 제곱의 합이 1로 표준화
4개의 변수들 간의 산점도
library(datasets)
data(USArrests)
pairs(USArrests, panel = panel.smooth, main = "USArrests data")
아래 결과를 보아 Murder와 UrbanPop비율간의 관련성이 작아 보인다
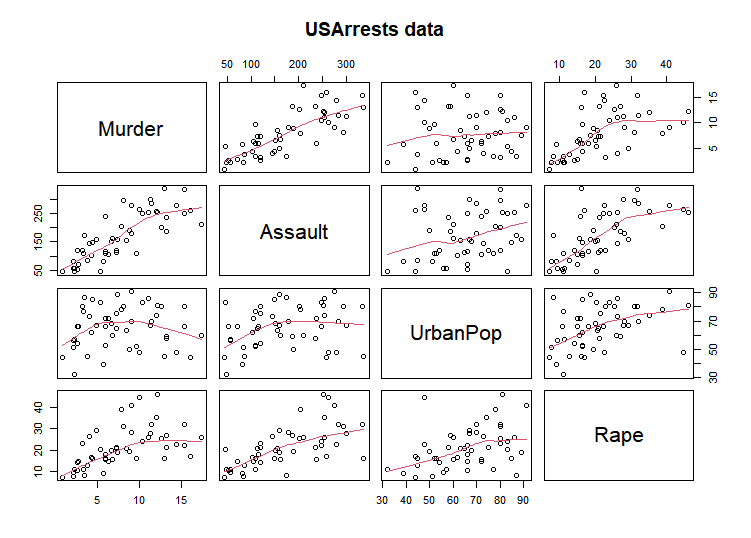
summary
US.prin <- princomp(USArrests, cor = TRUE)
summary(US.prin)
screeplot(US.prin, npcs=4, type = "lines")
아래 summary결과를 보면 제1주성분과 제2주성분까지의 누적분산비율은 대략 86.8%로 2개의 주성분 변수를 활용하여 전체 데이터의 86.6%를 설명할 수 있다
> summary(US.prin)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.5748783 0.9948694 0.5971291 0.41644938
Proportion of Variance 0.6200604 0.2474413 0.0891408 0.04335752
Cumulative Proportion 0.6200604 0.8675017 0.9566425 1.00000000
loading
- 네 개의 변수가 각 주성분 Comp.1-Comp.4까지 기여하는 가중치가 제시
- 제1주성분에서는 네 개의 변수가 평균적으로 기여
- 제2주성분에서는 Murder, Asaalut와 UrbanPop, Rape의 계수의 부호가 서로 다르다
```r
loadings(US.prin)
Loadings: Comp.1 Comp.2 Comp.3 Comp.4 Murder 0.536 0.418 0.341 0.649 Assault 0.583 0.188 0.268 -0.743 UrbanPop 0.278 -0.873 0.378 0.134 Rape 0.543 -0.167 -0.818
Comp.1 Comp.2 Comp.3 Comp.4 SS loadings 1.00 1.00 1.00 1.00 Proportion Var 0.25 0.25 0.25 0.25 Cumulative Var 0.25 0.50 0.75 1.00 ``` ### Scores 각 주성분 Comp.1-Comp.4의 선형식을 통해 각 지역별로 얻은 결과를 계산
> US.prin$scores
Comp.1 Comp.2 Comp.3 Comp.4
Alabama 0.98556588 1.13339238 0.44426879 0.156267145
Alaska 1.95013775 1.07321326 -2.04000333 -0.438583440
Arizona 1.76316354 -0.74595678 -0.05478082 -0.834652924
Arkansas -0.14142029 1.11979678 -0.11457369 -0.182810896
California 2.52398013 -1.54293399 -0.59855680 -0.341996478
Colorado 1.51456286 -0.98755509 -1.09500699 0.001464887
Connecticut -1.35864746 -1.08892789 0.64325757 -0.118469414
Delaware 0.04770931 -0.32535892 0.71863294 -0.881977637
Florida 3.01304227 0.03922851 0.57682949 -0.096284752
Georgia 1.63928304 1.27894240 0.34246008 1.076796812
Hawaii -0.91265715 -1.57046001 -0.05078189 0.902806864
Idaho -1.63979985 0.21097292 -0.25980134 -0.499104101
Illinois 1.37891072 -0.68184119 0.67749564 -0.122021292
Indiana -0.50546136 -0.15156254 -0.22805484 0.424665700
Iowa -2.25364607 -0.10405407 -0.16456432 0.017555916
Kansas -0.79688112 -0.27016470 -0.02555331 0.206496428
Kentucky -0.75085907 0.95844029 0.02836942 0.670556671
Louisiana 1.56481798 0.87105466 0.78348036 0.454728038
Maine -2.39682949 0.37639158 0.06568239 -0.330459817
Maryland 1.76336939 0.42765519 0.15725013 -0.559069521
Massachusetts -0.48616629 -1.47449650 0.60949748 -0.179598963
Michigan 2.10844115 -0.15539682 -0.38486858 0.102372019
Minnesota -1.69268181 -0.63226125 -0.15307043 0.067316885
Mississippi 0.99649446 2.39379599 0.74080840 0.215508013
Missouri 0.69678733 -0.26335479 -0.37744383 0.225824461
Montana -1.18545191 0.53687437 -0.24688932 0.123742227
Nebraska -1.26563654 -0.19395373 -0.17557391 0.015892888
Nevada 2.87439454 -0.77560020 -1.16338049 0.314515476
New Hampshire -2.38391541 -0.01808229 -0.03685539 -0.033137338
New Jersey 0.18156611 -1.44950571 0.76445355 0.243382700
New Mexico 1.98002375 0.14284878 -0.18369218 -0.339533597
New York 1.68257738 -0.82318414 0.64307509 -0.013484369
North Carolina 1.12337861 2.22800338 0.86357179 -0.954381667
North Dakota -2.99222562 0.59911882 -0.30127728 -0.253987327
Ohio -0.22596542 -0.74223824 0.03113912 0.473915911
Oklahoma -0.31178286 -0.28785421 0.01530979 0.010332321
Oregon 0.05912208 -0.54141145 -0.93983298 -0.237780688
Pennsylvania -0.88841582 -0.57110035 0.40062871 0.359061124
Rhode Island -0.86377206 -1.49197842 1.36994570 -0.613569430
South Carolina 1.32072380 1.93340466 0.30053779 -0.131466685
South Dakota -1.98777484 0.82334324 -0.38929333 -0.109571764
Tennessee 0.99974168 0.86025130 -0.18808295 0.652864291
Texas 1.35513821 -0.41248082 0.49206886 0.643195491
Utah -0.55056526 -1.47150461 -0.29372804 -0.082314047
Vermont -2.80141174 1.40228806 -0.84126309 -0.144889914
Virginia -0.09633491 0.19973529 -0.01171254 0.211370813
Washington -0.21690338 -0.97012418 -0.62487094 -0.220847793
West Virginia -2.10858541 1.42484670 -0.10477467 0.131908831
Wisconsin -2.07971417 -0.61126862 0.13886500 0.184103743
Wyoming -0.62942666 0.32101297 0.24065923 -0.166651801
제 1-2주성분에 의한 행렬도
arrests.pca <- prcomp(USArrests, center = TRUE, scale = TRUE)
biplot(arrests.pca, scale = 0)
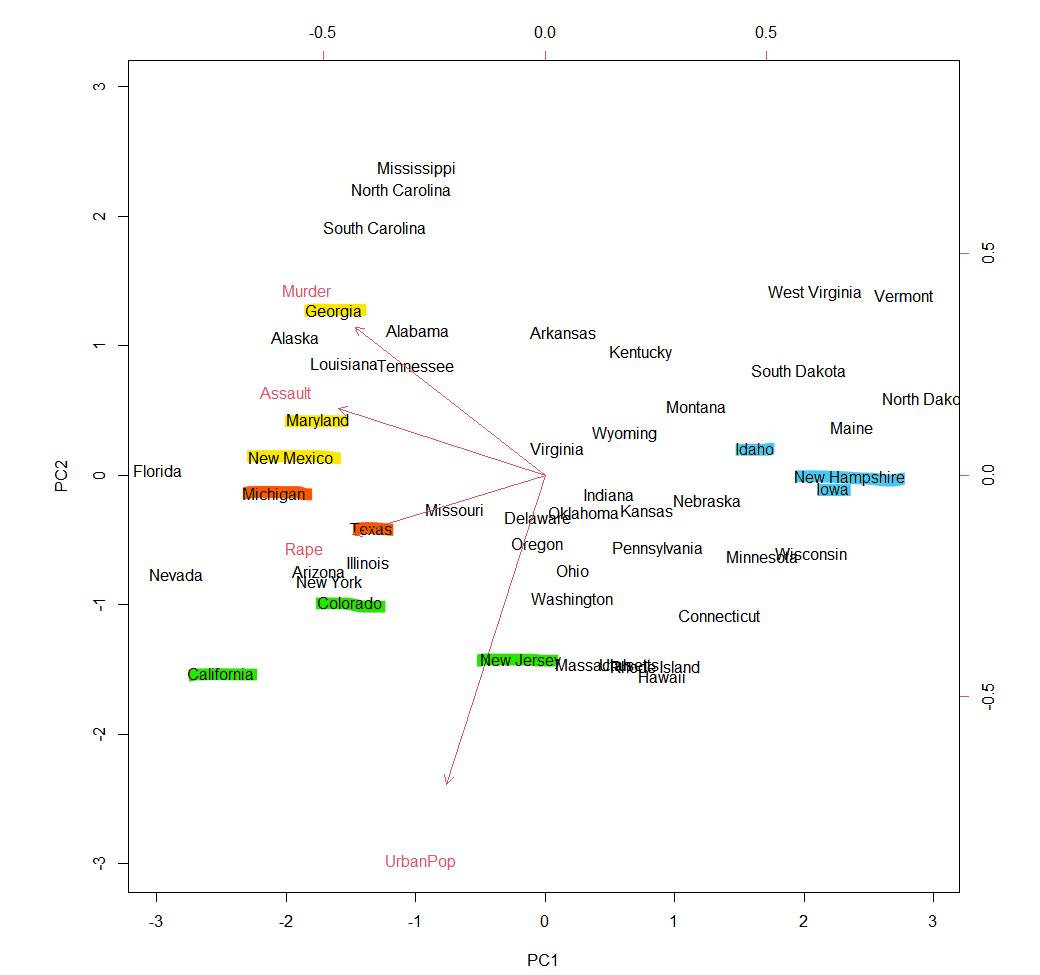
- 조지아, 메릴랜드, 뉴 멕시코 등은 폭행과 살인의 비율이 상대적으로 높은 지역
- 미시간, 텍사스 등은 강간의 비율이 높은 지역
- 콜로라도, 캘리포니아, 뉴저지 등은 도시에 거주하는 인구의 비율이 높은 지역
- 아이다호, 뉴 햄프셔, 아이오와 등의 도시들은 도시에 거주하는 인구의 비율이 상대적으로 낮으면서 3대 강력범죄도 낮음

댓글남기기